How Can The Mechanical Advantage Of An Inclined Plane, Or Ramp, Be Increased?

Mechanics: Describe, analyse and apply principles of uncomplicated machines and mechanical reward

Unit one: The mechanical advantage of an inclined plane

Leigh Kleynhans

By the finish of this unit of measurement you will be able to:

Describe, identify, and calculate the mechanical advantage of inclined planes.

 What you should know

Before you start this unit, make sure yous can:

Identify an inclined plane as a simple machine.

Introduction

In this unit you will build on your cognition of simple machines and forces to understand how an inclined plane offers . Y'all will also larn how to calculate the mechanical advantage of an .

Inclined planes are oft used when heavy objects need to be moved to a higher vertical position. Instead of lifting the object upwards, it tin can exist pushed up a ramp. There are many examples in everyday life where ramps are used to make a task easier.

How inclined planes create a mechanical advantage

For an inclined plane, less force is put into moving an object up the slope than if the object were lifted straight up, and so the mechanical advantage volition be greater than [latex]\scriptsize one[/latex]. The more than gradual the slope of the inclined plane, the less input force is needed and the greater the mechanical advantage.

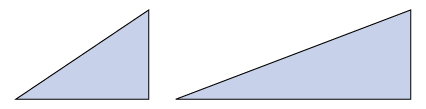
Figure 1: 2 planes with dissimilar angles of inclination

The inclined plane on the right has a more gradual gradient, and so it has a greater mechanical advantage. Less force is needed to move objects up the gentler slope, yet the objects attain the same height as they would if more strength were used to push button them up the steeper slope on the left.

There is a trade-off with this elementary machine. If the gradient is gentle, a person has to push button or pull the object over a longer distance, merely with little endeavour. If the slope is steep, a person has to push button or pull the object over a very curt distance, but with more effort.

What yous need:

small rocks
a sandwich pocketbook
a stack of books
a spring residue (If you lot exercise not accept a spring balance watch the video link at the stop of the action)
a ruler
a apartment piece of wood of minimum length [latex]\scriptsize 1\text{ m}[/latex]

What to practise:

Fill the sandwich bag with rocks and seal the bag.
Attach the hook of the spring balance through the tiptop of the sandwich.
Lift the bag vertically and read the force required to elevator the bag to a peak of [latex]\scriptsize 30\text{ cm}[/latex].
Place i finish of the flat slice of wood on the stack of books of summit [latex]\scriptsize xxx\text{ cm}[/latex] to make an inclined aeroplane.
Elevate the pocketbook of rocks, using the bound remainder up the slope and measure the force required.

What did yous detect?

The strength required to lift the bag of rocks vertically is greater than the force required to elevate it up the slope. The inclined airplane reduced the required effort force to raise the bag of rocks to a height of [latex]\scriptsize thirty\text{ cm}[/latex].

If yous do not have access to a spring rest, yous can watch a video of this experiment online.

Experiment (Duration: 01:fifteen)

Experiment

Computing mechanical advantage of inclined planes

To elevator an object vertically, the strength required would be equal to the weight of the object. ([latex]\scriptsize {{F}_{thou}}=mg[/latex]) and the object will gain gravitational potential energy ([latex]\scriptsize {{E}_{p}}=mgh[/latex]). Level 2 Subject Outcome 2.2 Unit of measurement 3 and Level 2 Subject Outcome two.3 Unit i

To push button an object up a frictionless inclined aeroplane, the force would be the endeavor (F_e) exerted over the distance up the plane. ([latex]\scriptsize W={{F}_{eastward}}50[/latex]). However, the gain in would withal be the same ([latex]\scriptsize {{Due east}_{p}}=mgh[/latex]).

Effigy 3: Raising an object using an inclined plane

Therefore:

[latex]\scriptsize \begin{align*}mgh&={{F}_{e}}L\\{{F}_{thou}}h&={{F}_{e}}L\cease{align*}[/latex]
and the platonic mechanical advantage ([latex]\scriptsize IMA[/latex]) can be expressed as [latex]\scriptsize \displaystyle \frac{{{{F}_{e}}}}{{{{F}_{e}}}}\text{ or }\displaystyle \frac{L}{h}[/latex].

As heights and lengths can exist easily measured, the following formula is most normally used to calculate the ideal mechanical advantage of an inclined plane:

[latex]\scriptsize IMA=\displaystyle \frac{L}{h}\text{ where: }L\text{ is the length of the plane and }h\text{ is the vertical height}[/latex]

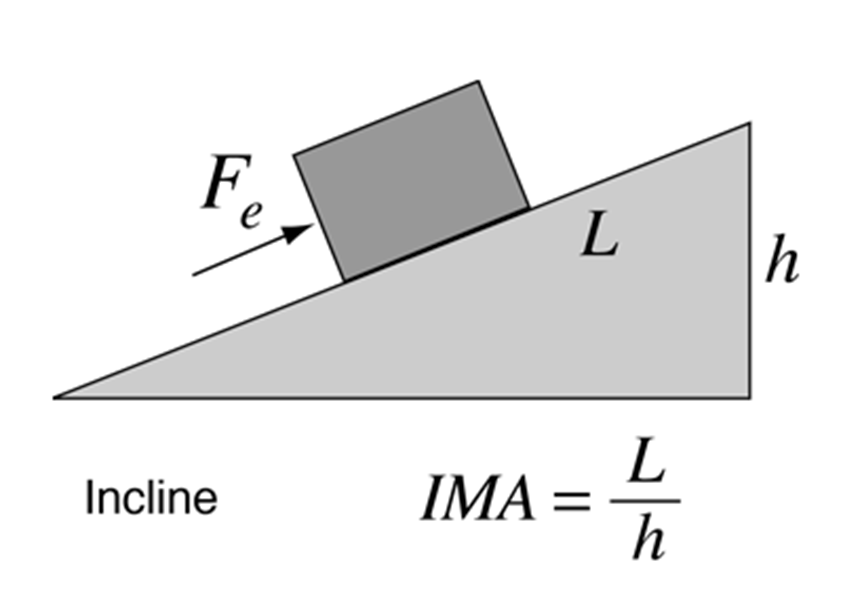
Figure iv: Calculating mechanical advantage of an inclined plane

In reality, there volition e'er be some energy 'lost' in overcoming friction when objects are pushed over surfaces.

Calculate the ideal mechanical reward of using a frictionless ramp of length [latex]\scriptsize 4\text{ m}[/latex] to raise a box to a platform with a vertical pinnacle of [latex]\scriptsize two.5\text{ one thousand}\text{.}[/latex]

Solution

Stride i: Write the formula

[latex]\scriptsize IMA=\displaystyle \frac{L}{h}[/latex]

Stride 2: Substitute the values and practice the calculation

[latex]\scriptsize \displaystyle \frac{four}{{2.five}}=1.six[/latex]

Note: there are no units for mechanical reward.

To consolidate your agreement, yous can picket this video to meet the mechanical reward of an inclined airplane when loading a box into the back of a van.

Summary

An inclined plane is a simple auto that consists of a sloping surface connecting a lower summit to a college elevation. It is used to move objects more easily to the higher height.
Less force is needed to move an object uphill with an inclined airplane, but the force must be applied over a greater altitude.
The mechanical advantage of an inclined plane is e'er greater than [latex]\scriptsize 1[/latex] because the machine puts out more force than the user puts into information technology.
The ideal mechanical reward of a frictionless inclined plane can exist calculated using the formula: [latex]\scriptsize IMA=\displaystyle \frac{L}{h}[/latex].

Suggested time to complete: 15 minutes

Explain how inclined planes act every bit uncomplicated machines.
The mechanical advantage of an inclined plane tin can be increased by:
1. shortening the path of the incline
2. enlarging the angle of the incline
3. minimising the angle of the incline
4. reducing the force used to movement objects
Summate the platonic mechanical reward of using the following frictionless inclined planes:
1. .
2. .
Calculate the ideal mechanical advantage of using the following frictionless inclined planes:
1. .
2. .
What is the height of the platform illustrated below if the platonic mechanical advantage provided past the ramp is 6?
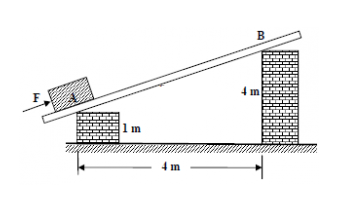
A learner pushes an object with a force of F from bespeak A to point B, every bit shown in the figure below. If the friction betwixt object and board is ignored, determine the mechanical advantage.
Proper noun three situations in everyday life where inclined planes are used.

The total solutions are at the end of the unit.

Unit one: Cess

Inclined planes reduce the strength required to motility an object up to a college level past increasing the distance over which the force acts.
C (minimising the angle of inclination)
.
Here is an caption:
.
The equation of mechanical advantage of the inclined plane is equally follows:
.
Mechanical reward = length of inclined airplane/summit of the inclined plane
- The mechanical advantage is straight proportional to the length of the inclined plane and therefore the mechanical advantage is enlarged if the length of the incline is enlarged.
- The mechanical reward is inversely proportional to the height of the inclined plane; therefore, the mechanical advantage is minimised if the pinnacle of the inclined plane is enlarged and the mechanical advantage is enlarged if the height of the incline is reduced.
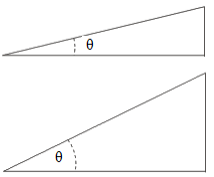
-  If the angle is minimised and so the summit of the inclined plane is reduced. The mechanical advantage is enlarged if the height of the inclined plane is reduced. Hence if the angle is minimised then the mechanical advantage is enlarged.
- If the bending is enlarged then the meridian of the inclined plane is enlarged. The mechanical advantage is minimised if the height of the inclined plane is enlarged. Hence if the angle is enlarged then the mechanical advantage is minimized.
.
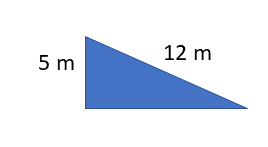
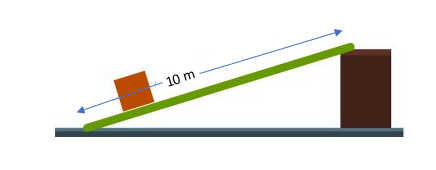
1. [latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{{12}}{5}=2.iv[/latex]
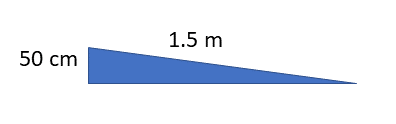
2. [latex]\scriptsize 50\text{ cm = 0}\text{.five one thousand}[/latex]
  [latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{{i.5}}{{0.v}}=3[/latex]
.
1. Utilize Pythagoras to notice [latex]\scriptsize Fifty[/latex]:
  [latex]\scriptsize \begin{marshal*}{{50}^{ii}}&={{2}^{ii}}+{{6}^{2}}\\L&=six.32\text{ m}\end{align*}[/latex]
  [latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{{6.32}}{2}=three.xvi[/latex]
2. Use Pythagoras to find [latex]\scriptsize h[/latex]:
  [latex]\scriptsize \begin{align*}{{7}^{2}}&={{v}^{2}}+{{h}^{2}}\\h&=4.9\text{ yard}\end{align*}[/latex]
  [latex]\scriptsize IMA=\displaystyle \frac{50}{h}=\displaystyle \frac{{4.9}}{two}=2.45[/latex]
.
[latex]\scriptsize \begin{align*}IMA&=\displaystyle \frac{L}{h}\\\text{ }6&=\displaystyle \frac{{10}}{h}\\\text{ }h&=\text{one}\text{.67 m}\end{align*}[/latex]
Height of inclined plane [latex]\scriptsize =4-1=3\text{ yard}[/latex]
Length of horizontal plane [latex]\scriptsize 4\text{ k}[/latex]
Utilize Pythagoras to calculate length of the inclined plane:
[latex]\scriptsize \begin{align*}{{50}^{2}}&={{3}^{ii}}+{{iv}^{ii}}\\L&=5\text{ m}\stop{marshal*}[/latex]
[latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{5}{3}=one.67[/latex]
.
- loading ramps
- wheelchair ramps
- stairs
- escalators
- inclined conveyor belts
- ladders
- roads to high elevations
- or any other appropriate examples.

Dorsum to Unit 1: Assessment